What is a Maths Formula?
Formulae in GCSE Maths are algebraic rules expressed through mathematical symbols. Mathematical formulae range from the more simplistic (geometry, algebra and trigonometry) to the more complex: calculating quadratic equations.
Importance of Learning GCSE Maths Formulas
Mastering GCSE maths formulas is paramount for success in exams. In the upcoming year, GCSE students will no longer have the luxury of a formula sheet during exams, underscoring the urgency of thoroughly comprehending and memorizing these essential mathematical tools. This blog post aims to facilitate this process by showcasing key formulas for revision and exam preparation.
What are the Essential Formulae for GCSE Maths Exams?
This section delves into fundamental formulas crucial for GCSE Maths exams, covering areas such as geometry and trigonometry.
Area of a Rectangle
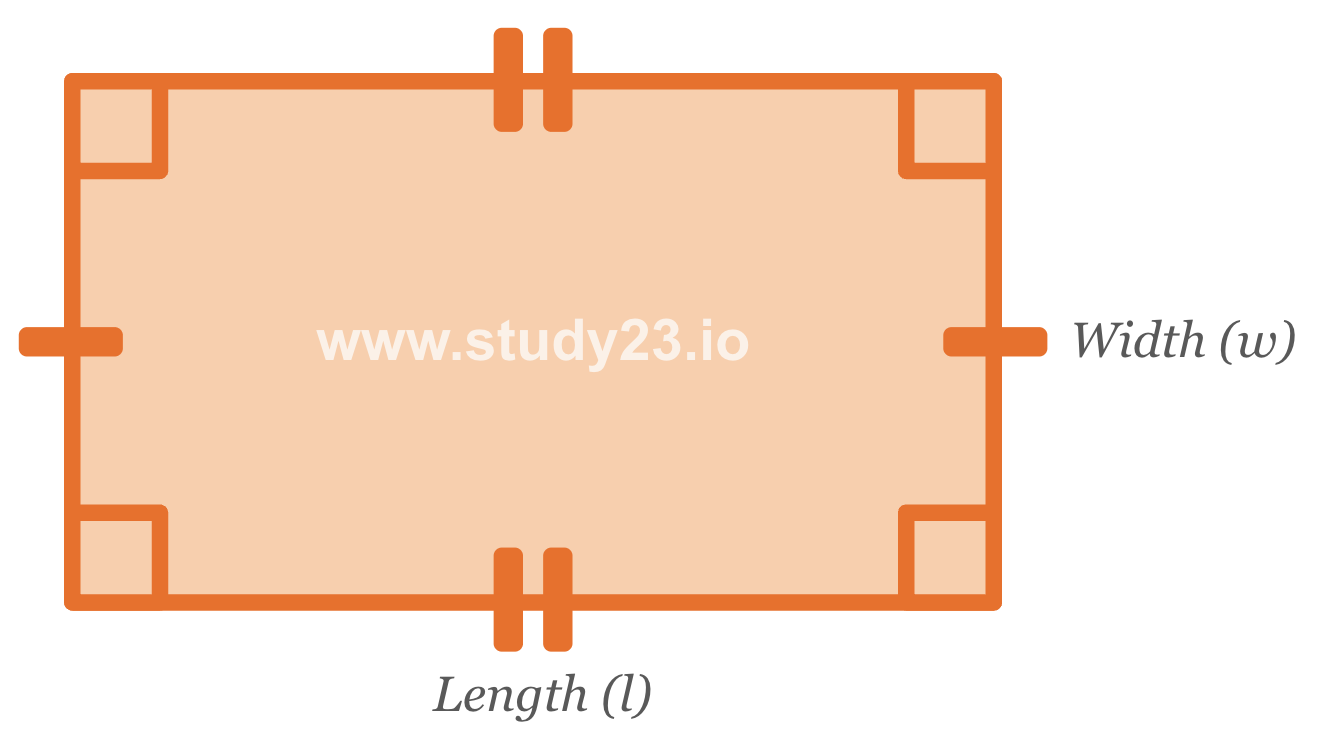
The formula for calculating the area of a rectangle is: \( \text{Length} \times \text{Width} \)
Levels: Foundation & Higher
Area of a Parallelogram
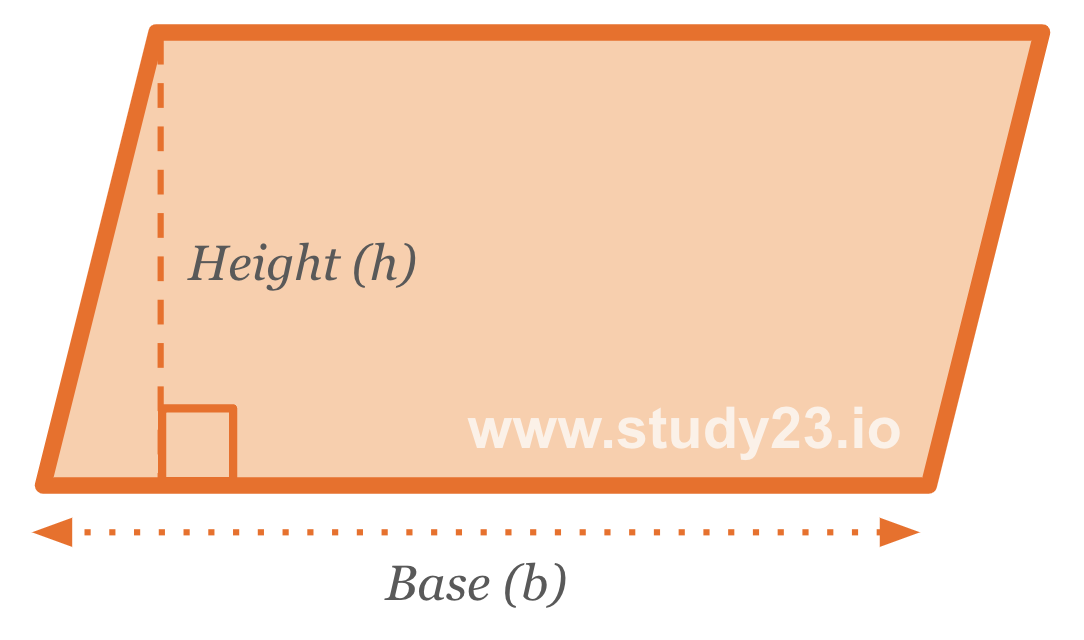
The formula for calculating the area of a parallelogram is: \( \text{Base} \times \text{Height} \)
Levels: Foundation & Higher
Area of a Triangle
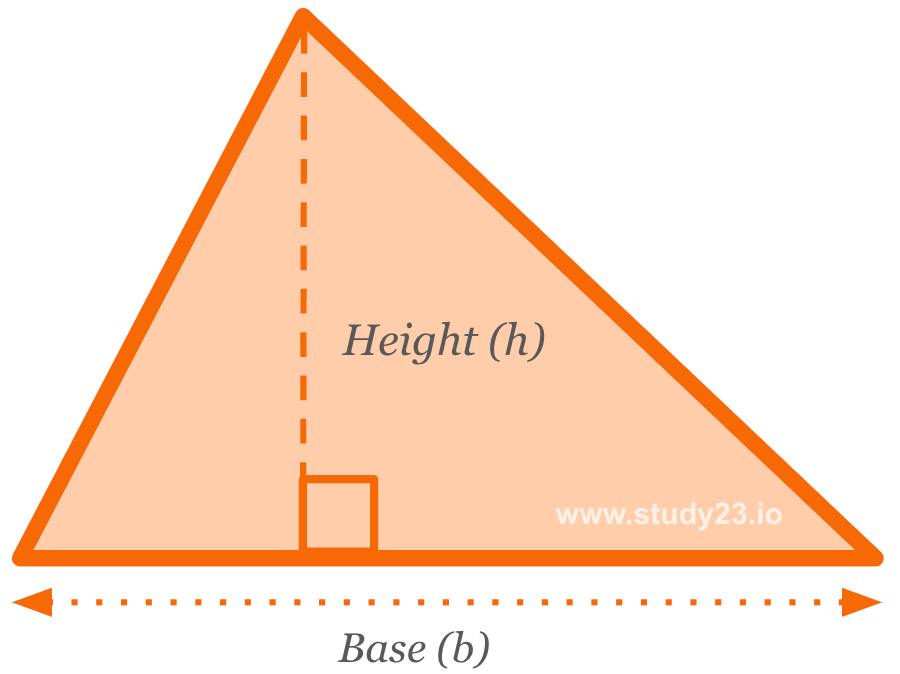
The formula for calculating the area of a triangle is: \( \frac{1}{2} \times \text{Base} \times \text{Height} \)
Levels: Foundation & Higher
Area of a Trapezium
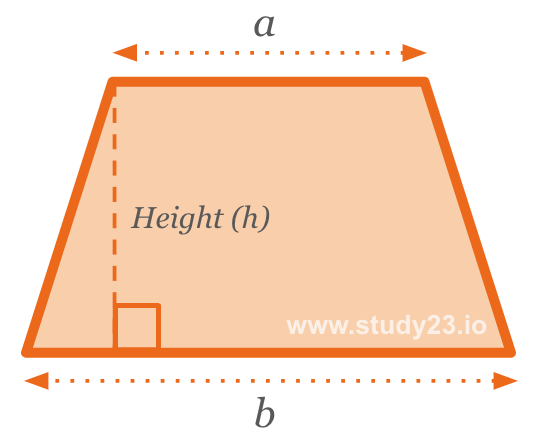
The formula for calculating the area of a trapezium is: \( \frac{1}{2} \times \text{(a+b)} \times \text{Height} \)
Levels: Foundation & Higher
Circumference of a Circle
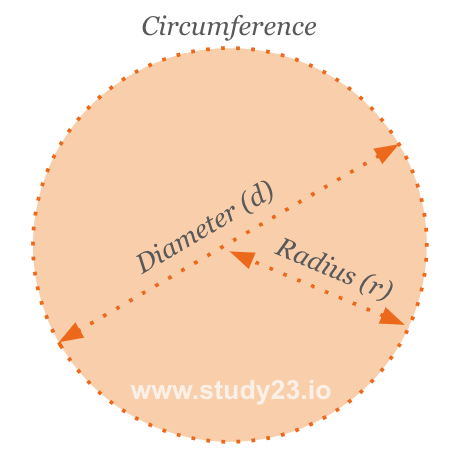
There are two formulas for calculating the circumference of a circle:
- Using the diameter: \( \text{Circumference} = \pi \times \text{d} \)
- Using the radius: \( \text{Circumference} = 2 \pi \times \text{r} \)
Levels: Foundation & Higher
Area of a Circle

The formula for calculating the area of a circle is: \( \pi \times \text{r}^2 \)
Levels: Foundation & Higher
Volume of a Cuboid
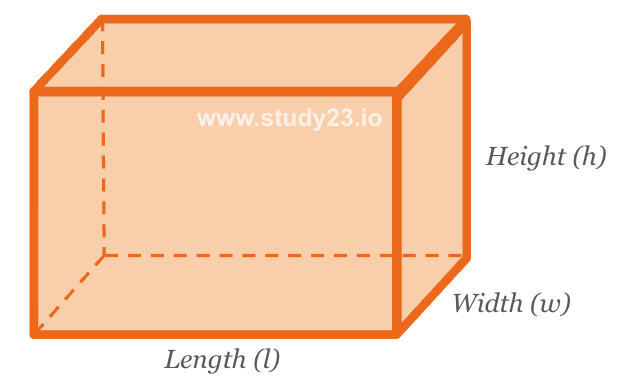
The formula for calculating the volume of a cuboid is: \( \text{Length} \times \text{Width} \times \text{Height} \)
Levels: Foundation & Higher
Volume of a Prism
The formula for calculating the volume of a prism is: \( \text{Area of cross section} \times \text{Height} \)
Levels: Foundation & Higher
Volume of a Cylinder
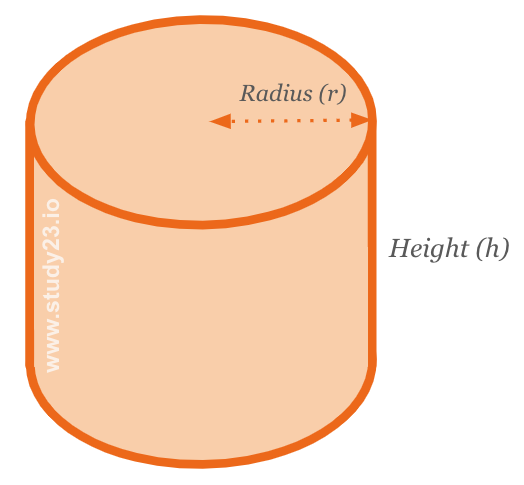
The formula for calculating the volume of a cylinder is: \( \pi \times \text{r}^2 \times \text{h} \)
Levels: Foundation & Higher
Volume of a Pyramid
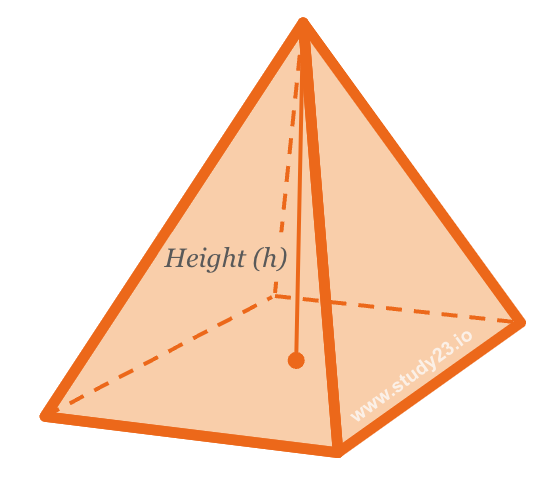
The formula for calculating the volume of a pyramid is: \( \frac{1}{3} \times \text{Area of base} \times \text{Height} \)
Level: Higher
Pythagoras’ Theorem
The formula for calculating the length of the hypotenuse of a right-angled triangle is: \( \text{a}^2 + \text{b}^2 = \text{c}^2 \ \)
Levels: Foundation & Higher
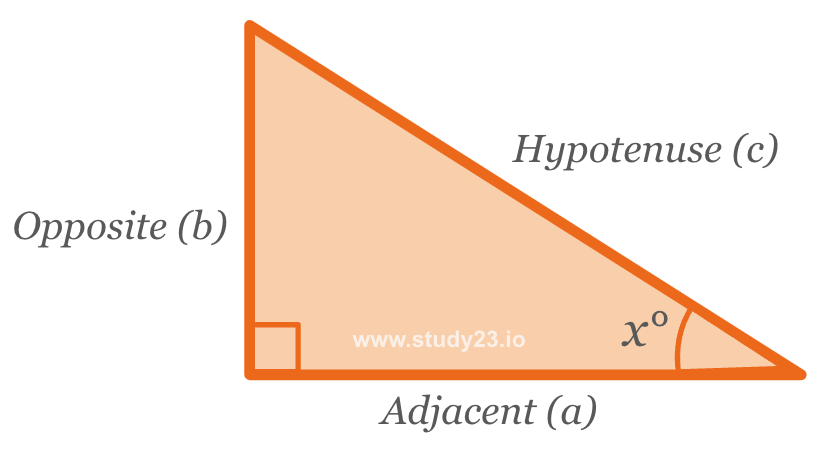
Trigonometry (SOH CAH TOA)

There are three formulas for calculating the length of a side of a right-angled triangle:
- SOH: \( \text{sin} \theta = \frac{\text{opposite}}{\text{hypotenuse}} \)
- CAH: \( \text{cos} \theta = \frac{\text{adjacent}}{\text{hypotenuse}} \)
- TOA: \( \text{tan} \theta = \frac{\text{opposite}}{\text{adjacent}} \)
Levels: Foundation & Higher
Trigonometry (Sine Rule)
The formula for calculating the length of a side of a non-right-angled triangle is: \( \frac{\text{a}}{\text{sin}A} = \frac{\text{b}}{\text{sin}B} = \frac{\text{c}}{\text{sin}C} \)
Level: Higher
Trigonometry (Cosine Rule)
The formula for calculating the length of a side of a non-right-angled triangle is: \( \text{a}^2 = \text{b}^2 + \text{c}^2 - 2bc \times \text{cos}A \)
Level: Higher
Area of a Non-Right-Angled Triangle
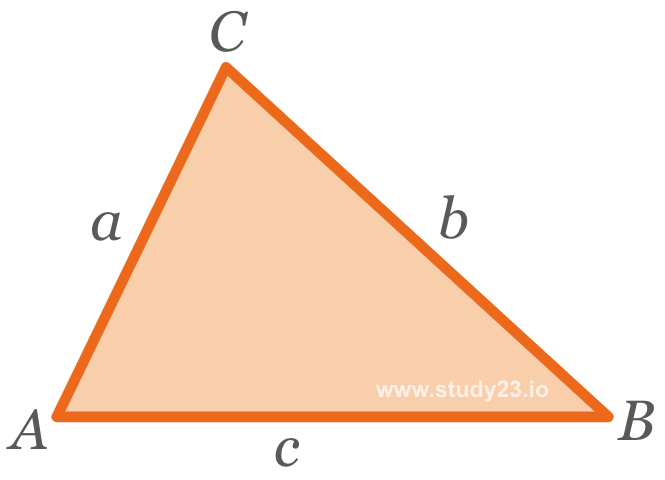
The formula for calculating the area of a non-right-angled triangle is: \( \frac{1}{2} \times ab \times \text{sinC} \)
Level: Higher
Compound Measures
The formula for calculating compound measures are:
- Speed: \( \text{Speed} = \frac{\text{Distance}}{\text{Time}} \)
- Density: \( \text{Density} = \frac{\text{Mass}}{\text{Volume}} \)
- Pressure: \( \text{Pressure} = \frac{\text{Force}}{\text{Area}} \)
Levels: Foundation & Higher
Quadratic Equations
The solutions for \( ax^2 + bx + c = 0 \) where \( a \neq 0 \) are given by \( \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \)
Level: Higher
Final Thoughts
The importance of GCSE Maths formulas in achieving exam success cannot be overstated. By dedicating time to grasp these mathematical concepts, students can enhance their problem-solving skills and improve their chances of excelling in their GCSE Maths exams. Happy studying!
Study23 GCSE Maths Formula Flash Cards
There are a lot of GCSE Maths formulae to learn. The Study23 GCSE Maths Formula Flash Cards help with memorising the formulas for your GCSE Maths exams.
Related Posts
- A Glossary of GCSE Maths Terms
- GCSE Maths Formula Sheet: Higher and Foundation Level Maths Formulas
- 10 Free Learning Resources for GCSE Maths
- Boost GCSE Scores: The Maths Flash cards Advantage
- Break Free from Math Anxiety - A Holistic Approach During Your GCSEs Revision Journey